1
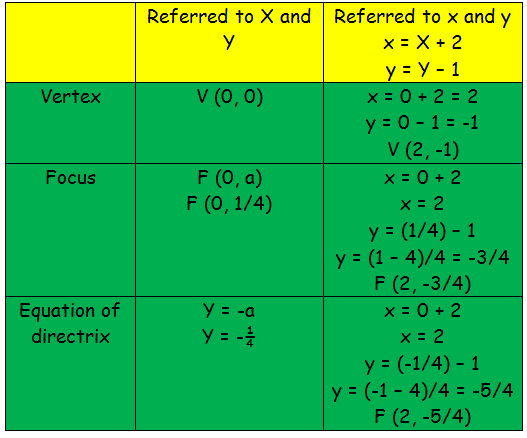
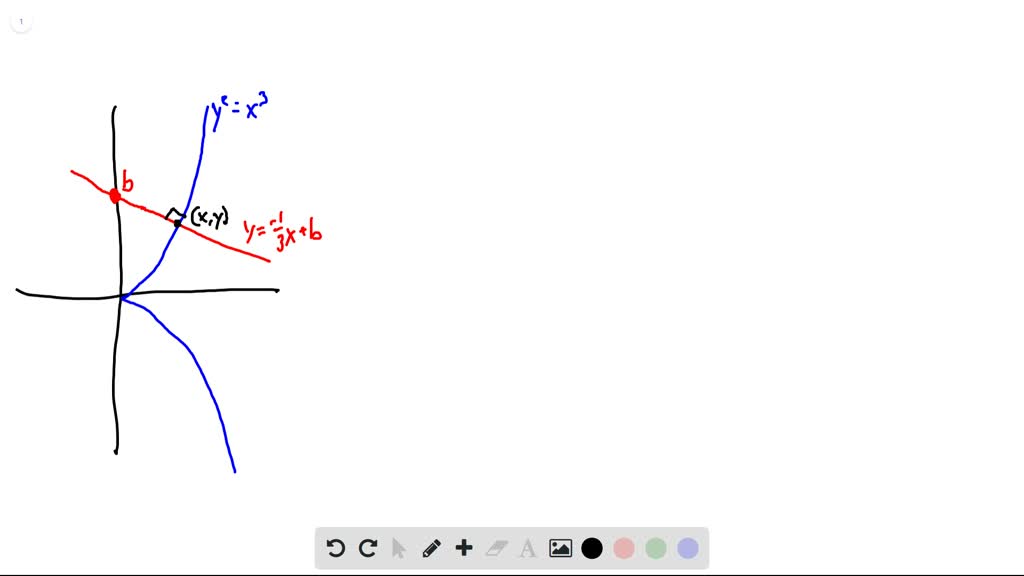
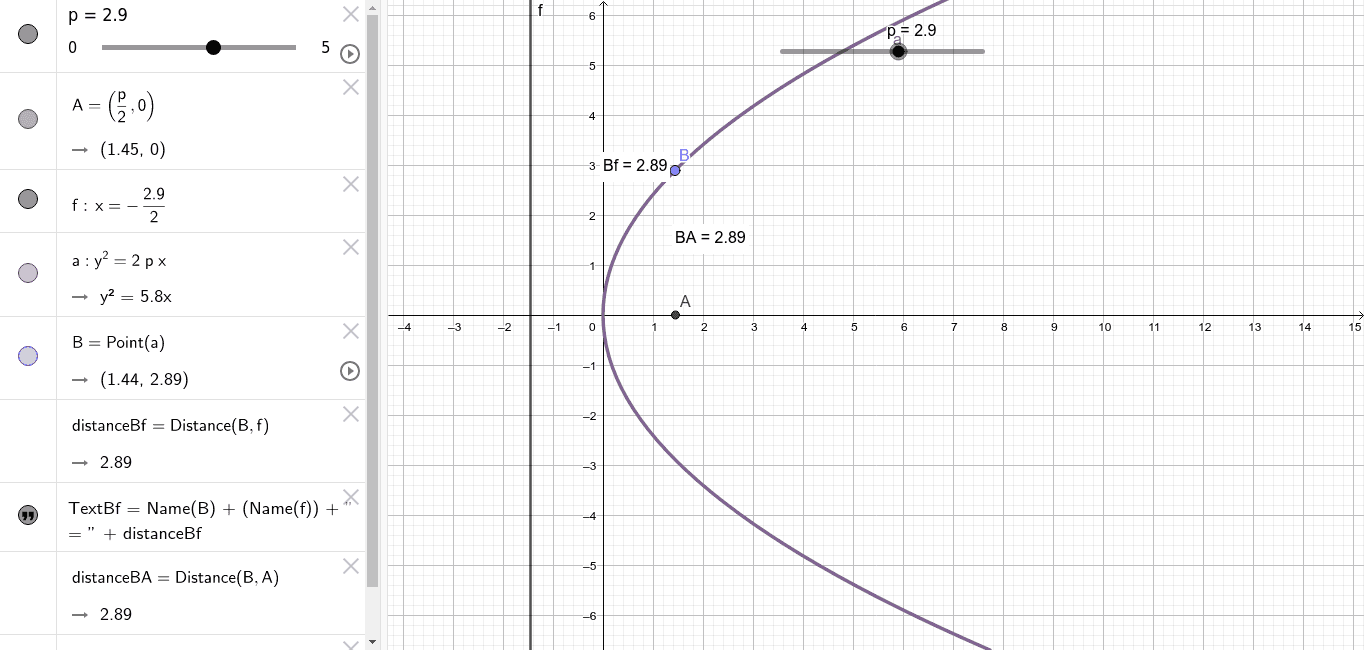
Get an answer for 'Find the point on the parabola xy^2=0 that is closest to the point (0,3)' and find homework help for other Math questions at eNotesLa ecuación de la parábola la podemos expresar del modo siguiente y 2 = 8/3 x De donde se deduce que 4a 8 3 = de donde a 2 3 = El foco esta dado pues por el punto de coordenadas (2/3, 0) y la ecuación de la directriz es x = −2/3 Para hallar la longitud del lado recto se calcula el valor de "y" para x = 2/3 Si x = 2/3 se
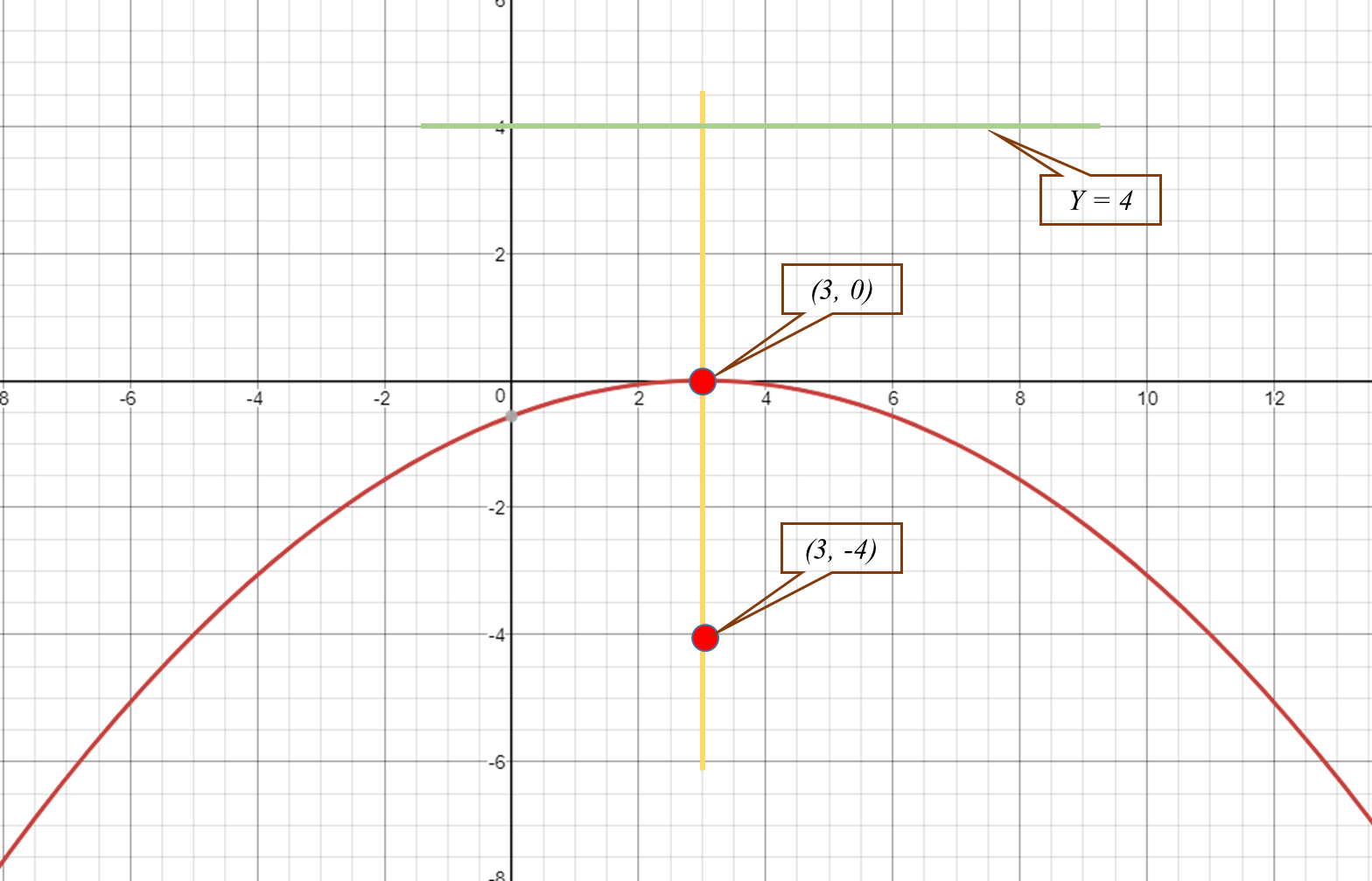
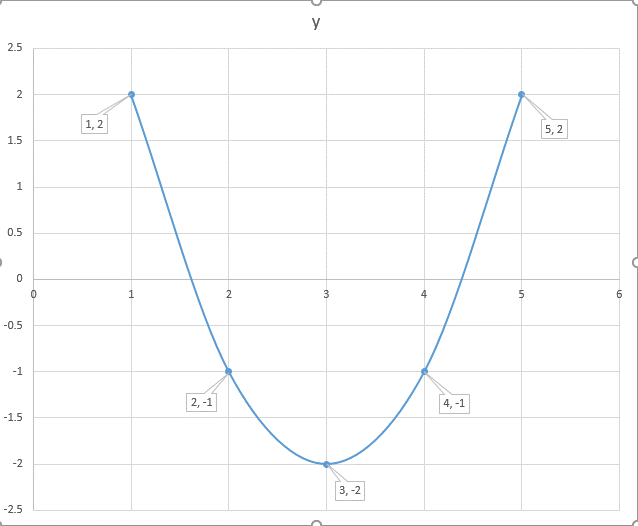
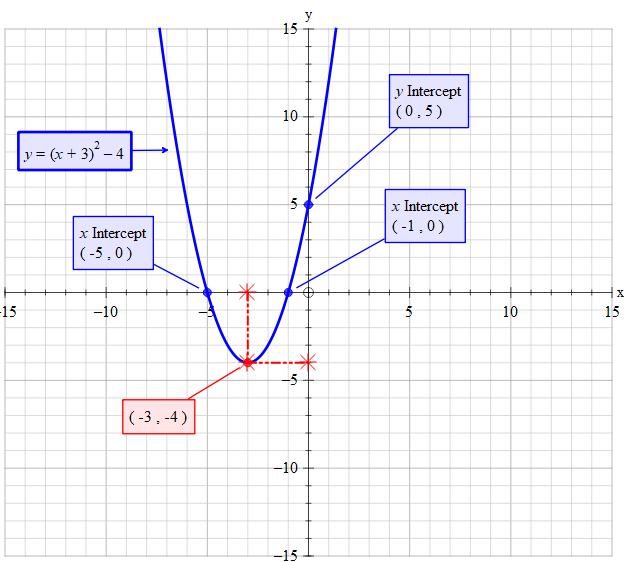
Parabola y=-2(x-3)^2+4 ma dwa punkty
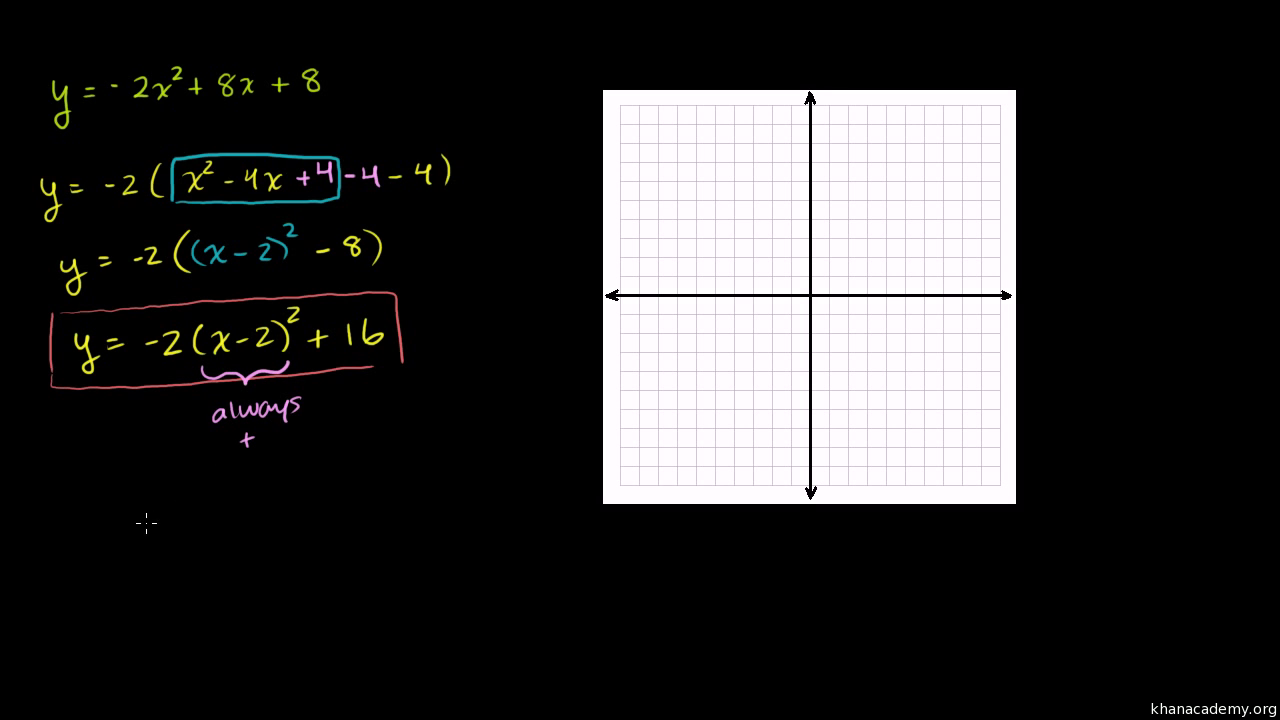
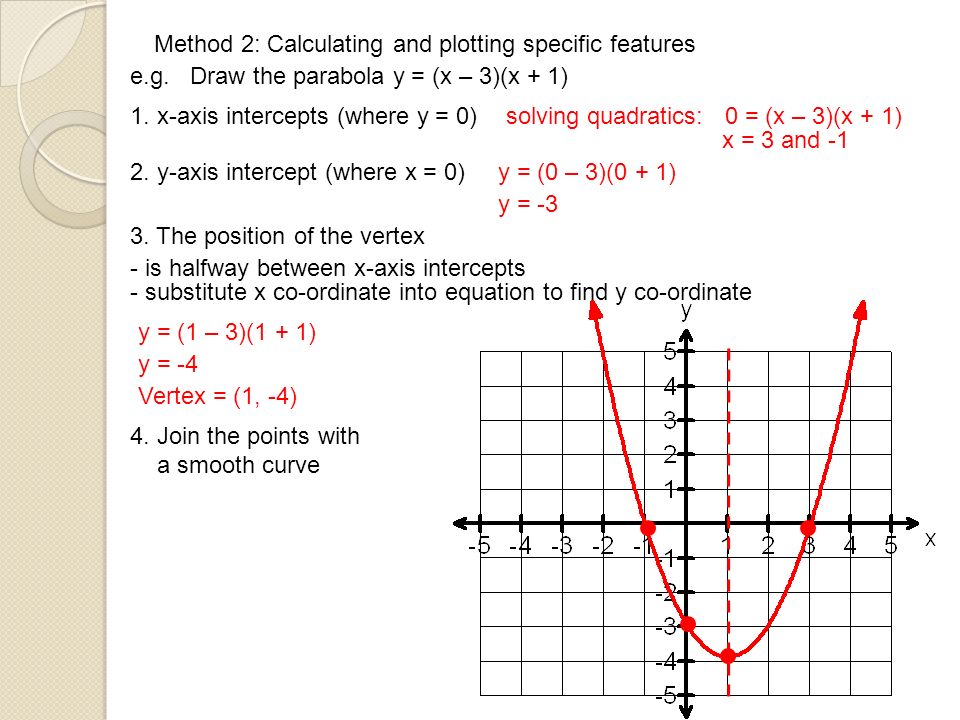
Parabola y=-2(x-3)^2+4 ma dwa punkty-We can find the parabola's equation in vertex form following two steps Step 1 use the (known) coordinates of the vertex, ( h, k), to write the parabola 's equation in the form y = a ( x − h) 2 k the problem now only consists of having to find the value of the coefficient a Step 2 find the value of the coefficient a by substitutingSehingga, bentuk umum persamaannya x 2 = 4py Karena titik fokusnya di F(0,5), maka p=5 Jadi persamaan parabola x 2 = 4py, sehingga persamaan parabola x 2 = y 9 Tentukan titik fokus, garis direktis, dan latus rectum dari parabola 2x 2 32y=0 Jawab Parabola Vertikal dengan Puncak O(0, 0) 2x 2 32y = 0 2x 2 = 32y x 2 = 16y x 2 = 4py 4p

The Equation To The Line Touching Both The Parabolas Y 2 4x And X 2 32y Is
Correct option is B) Given equation is λx 24xyy 2λx3y2=0 Compairing with ax 2by 22hxy2gx2fyc=0 Here a=λ,b=1,h=2 For given equation to be an equation of a parabola we must have h 2=ab ⇒2 2=1λ ⇒λ=4Take the square root of both sides of the equation x^{2}3=y Swap sides so that all variable terms are on the left hand side x^{2}3y=0 Subtract y from both sides x=\frac{0±\sqrt{0^{2}4\left(3y\right)}}{2} This equation is in standard form ax^{2}bxc=0We have any point on the axis as ( h, k), hence the condition is h > 3 ( a c 2) = 3 ( 1 0 2) = 3 2 So the correct option is A Note The condition for k is k > 3 4 We can alternatively solve by shifting the standard parabola y 2 = 4 a x by 45 ∘ in an anticlockwise direction The equation of normals to the parabola y 2 = 4 a x with
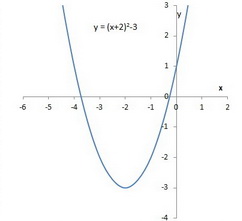
When graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if aParábola (y3)^2=12(x1) Se muestra la ecuacion de una parabola en su forma reducida (y3)^2=12(x1) Se determina vertice, foco y 2x²3 a=2 , b=0 c=3 v = 0/2(2)=0 Remplazas x= 0 para encontrar las coordenadas del punto donde se encuentra el vértice p=(03) En la gráfica puedes analizar mejor el problema Saludos Publicidad Publicidad gabrielabetancourt27 gabrielabetancourt27 Respuesta holaaaaaaaaaaaaaaaaaaaaaaa
Parabola y=-2(x-3)^2+4 ma dwa punktyのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
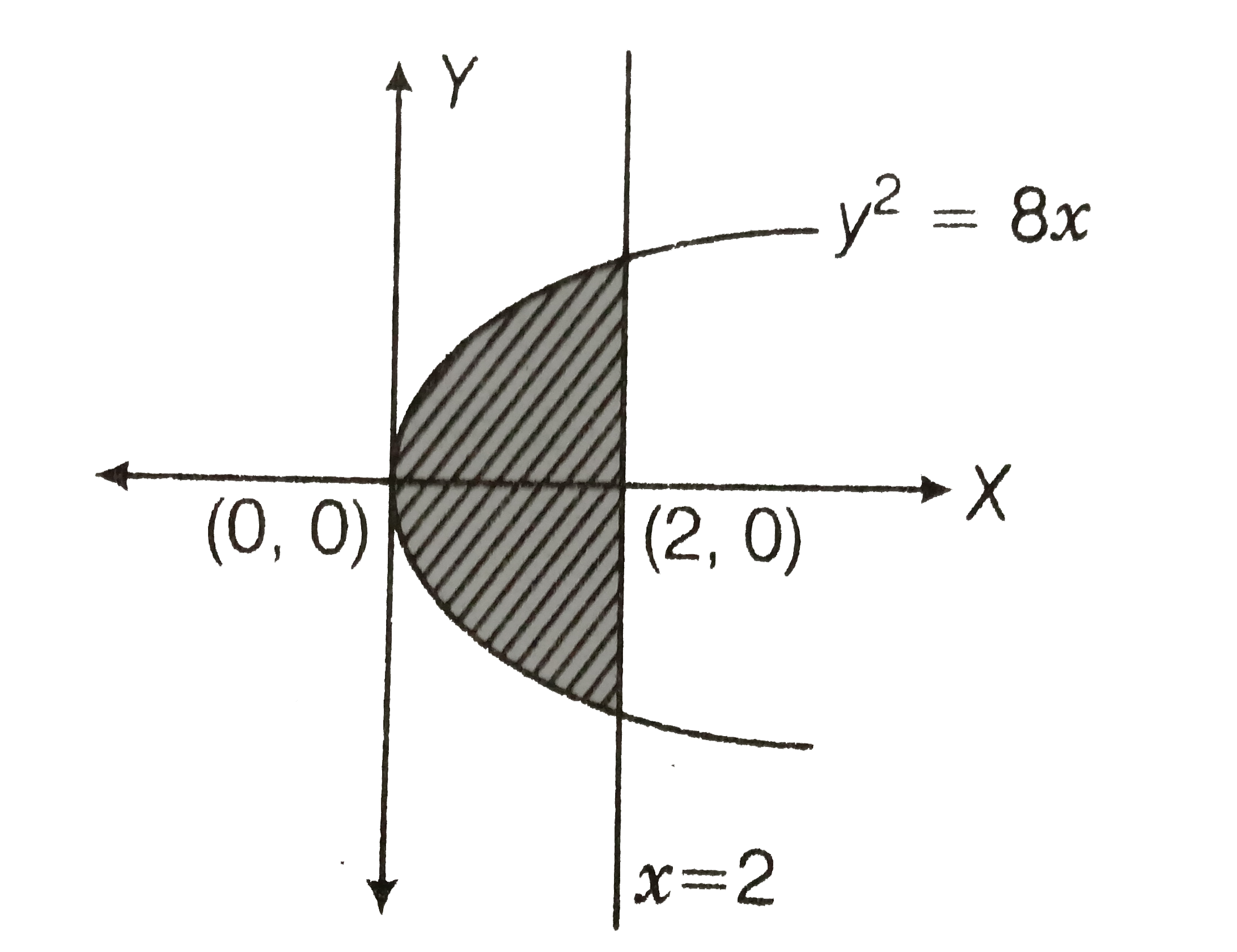 |  | |
 |  | |
 |  | |
「Parabola y=-2(x-3)^2+4 ma dwa punkty」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
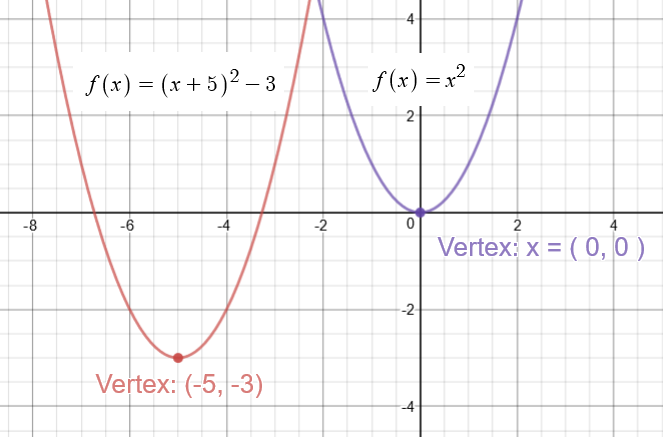
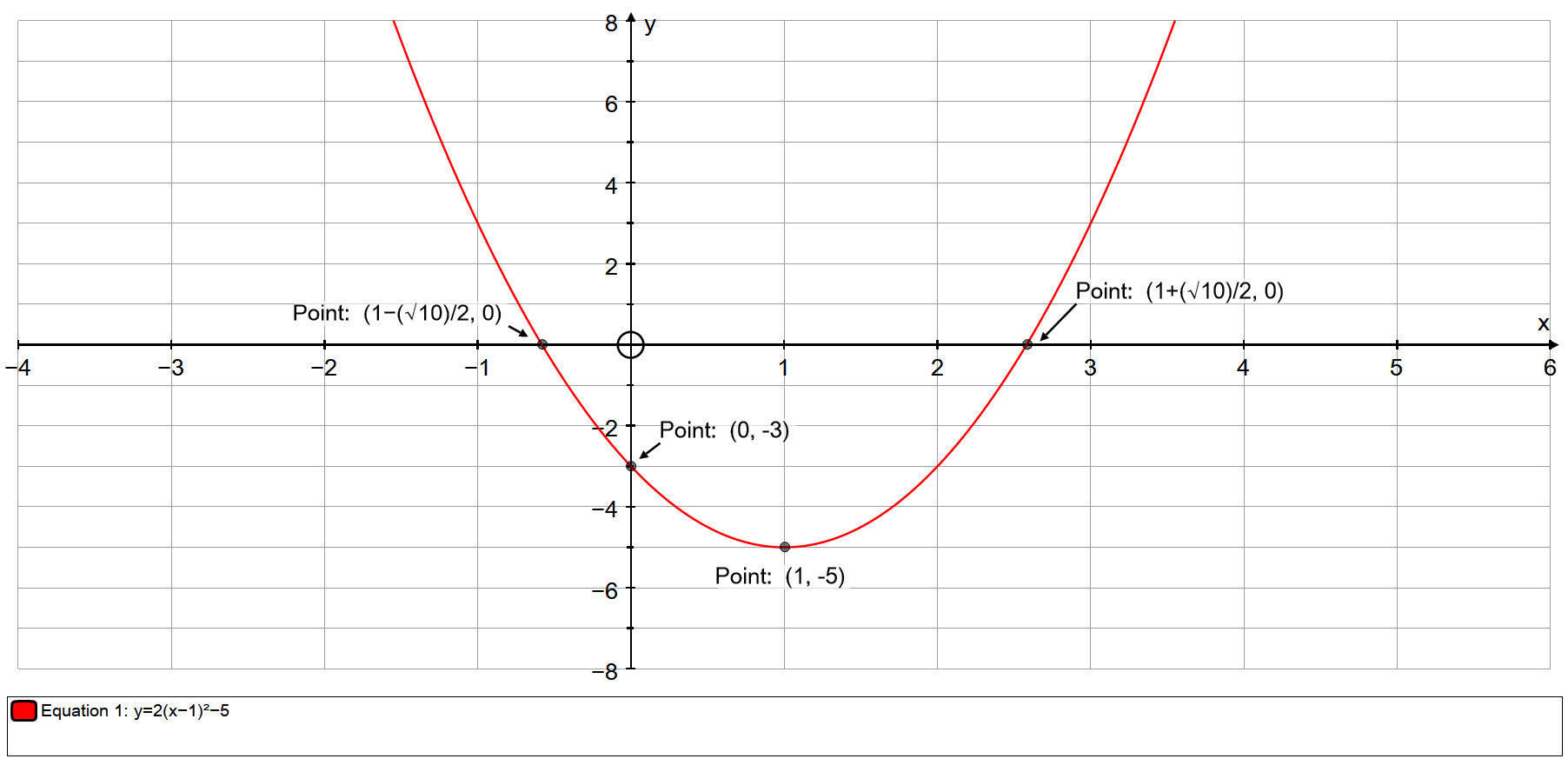
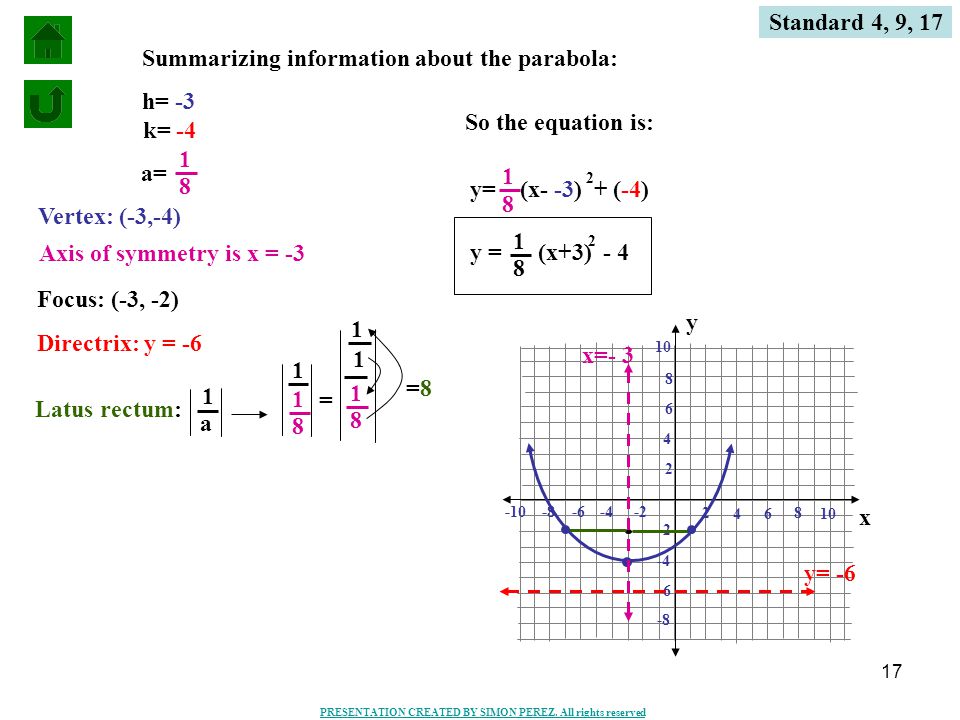
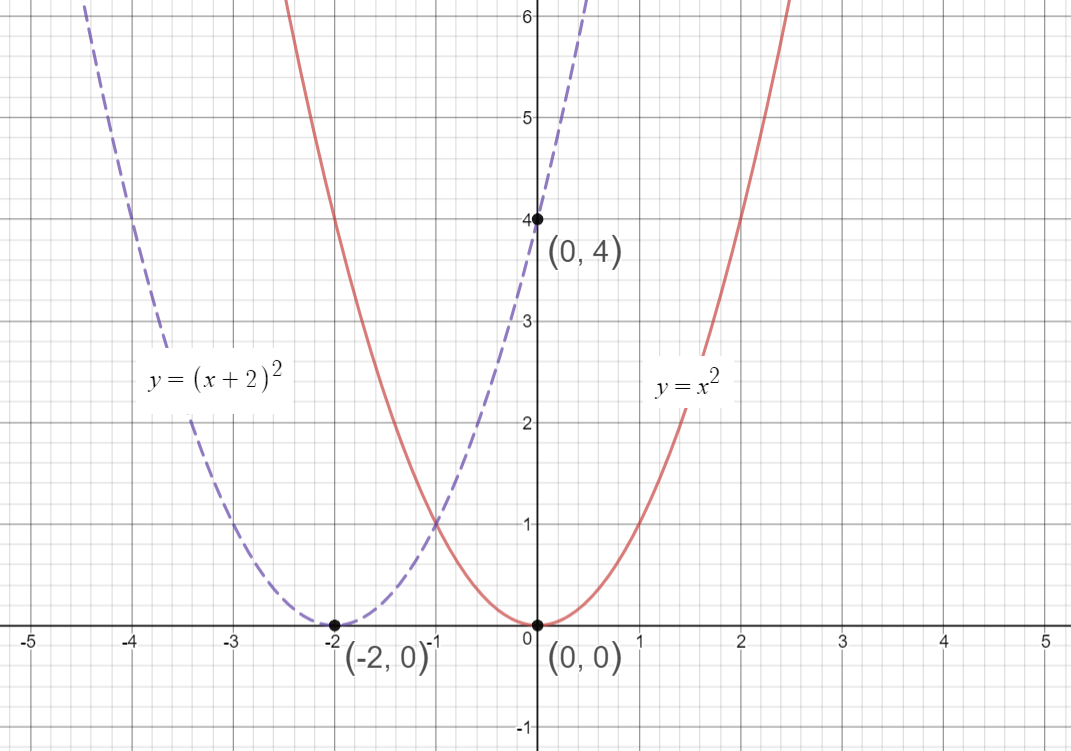
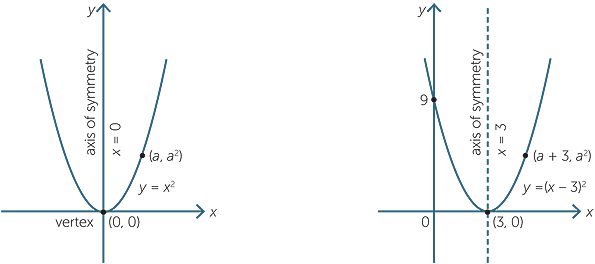
Although there may be some other methods, but I found it the most intuitive of all and takes only 10 seconds more than several other methods that use the properties of parabola ) You'll get α= 3/2 = β So the axis of the parabola is the line y=x Hence, directrix is y= x The focus, as it lies on the axis, will be (say) (p,p)Learn the rule y = a(x h)² k has vertex (h, k) Notice that h has the OPPOSITE sign from the sign just before it, and that k has the SAME sign that is before it What is the vertex of the parabola defined byy = 2(x 3)² 5 The 3 has a before it so we use the OPPOSITE sign The 5 has a before it so we use the SAME sign
Incoming Term: graph the parabola y=(x-3)^2+2, (y-2)^2=4(x+3) parabola, parabola y=-2(x-3)^2+4 ma dwa punkty wspólne, parabola y=-2(x-3)^2+4 ma dwa punkty,




0 件のコメント:
コメントを投稿